线性代数-行列式
主对角线:从左上到右下
副对角线:从右上到左下
行列式的性质:
- 行列式转置不变
- k乘一个行列式,等于乘以这个行列式的某一行(列)(矩阵等于乘以这个矩阵的所有元)
- 如果行列式一行(列)元素都是两数之和,则D可以写为两个行列式之和
- 行列式两行(列)元素相同,则这个行列式为零(可以看作是第五点的特殊情况)
- 行列式两行(列)元素成比例,则这个行列式为零
- 把行列式的某一行(列)的倍数加到另一行,行列式不变
- 互换行列式的两行(列),行列式变号(正负号)
行列式的展开
在n阶行列式中,划去$a_{ij}$所在的第i行和第j列,余下的元素排成n-1阶行列式,称为$a_{ij}$的余子式,记作$M_{ij}$;$A_{ij}=(-1)^{i+j}M_{ij}$,称为$a_{ij}$的代数余子式
$D=a_{ij}A_{ij}$(当某一行(列)只有$a_{ij}$不为零,其余都为零时成立.可以看作是第二点的特殊情况)
n阶行列式$D=\left | a_{ij} \right |$等于其任意一行的各元素与对应代数余子式乘积之和
n阶行列式D的某一行(列)的元素与另一行(列)对应的代数余子式乘积之和等于零
余子式概念的推广:在n阶行列式D中,划去其某个k阶子式N所在的行及所在的列,得到的n-k阶子式M,称为N的余子式代数余子式概念的推广:若N所在行的顺序是$i_{1},i_{2},…,i_{k}$,所在列的顺序为$j_{1},j{2},…,j{k}$,则N的代数余子式为:$(-1)^{i_{1}+i_{2}+…+i_{k}+j_{1}+j_{2}+…+j_{k}}M$拉普拉斯(Laplace)展开定理:在n阶行列式D中,取定某k个行($1≤k≤n$),则在这k个行中所有k阶子式分别与它的代数余子式乘积之和等于D.说明:
在计算行列式时,常常按一行或一列展开,若在行列式D中某些行或某些列含多个零元素,则按这些行或这些列展开计算行列式可能更方便.
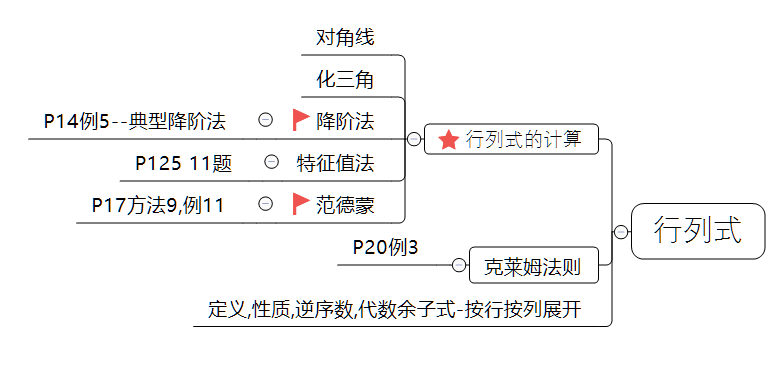
行列式的计算
- 定义法 较多零元素的高阶行列式可用
- 性质法 利用行列式的性质
- 降阶法 利用行列式按行(列)展开和拉普拉斯定理
- 化零降阶法 利用性质对行列式进行变换,使某行(列)元素仅留一个非零,其余全为零,然后用降阶法
说明:
为了用好化零降阶法,常常是从含绝对值最小的整数所在的行(列)开始,如含1或-1所在的行(列)
在化零过程中应尽量避免出现分数
若某行(列)的元素偏大时,先用性质将它们变小
三角形法 利用上(下)三角形行列式的结论
升阶法 亦叫加边法、镶边法等
归纳法
递推法
范德蒙(Vander Monde)法 利用范德蒙行列式的结果计算行列式
范德蒙行列式:
$$
\begin{vmatrix}
1 & 1 & … & 1\
a_{1} & a_{2} & … &a_{n} \
a_{1}^2 & a_{2}^2 & … & a_{3}^2\
… & …&… & …\
a_{1}^{n-1} & a_{2}^{n-1} & … &a_{n}^{n-1}
\end{vmatrix}=\prod_{1\leqslant j \leqslant i\leqslant n}(a_{i}-a_{j})
$$反对称法 奇数阶反对称行列式等于零
定义:在D=|a
ij|中,如果$a_{ij}=a_{ji}$,则称D为对称行列式.如果$a_{ij}=-a_{ji}$,则称D为*反对称行列式
行列式的应用
非齐次线性方程组\系数行列式:
$
a_{11}x_{1}+a_{12}x_{2}+…+a_{1n}x_{n}=b_{1},
$
$
a_{21}x_{1}+a_{22}x_{2}+…+a_{2n}x_{n}=b_{2},
$
$
……
$
$
a_{m1}x_{1}+a_{m2}x_{2}+…+a_{mn}x_{n}=b_{n}
$
若$b_{i}(i=1,2,…,n)$不全为零,则称该方程为非齐次线性方程组,其系数构成的行列式$D=\begin{vmatrix} a_{11} & a_{12} & … & a_{1n}\
a_{21} & a_{22} & … &a_{2n} \ … & …&… & …\
a_{n1} & a_{n2} & … &a_{nn} \end{vmatrix} $称为该方程组的系数行列式
克莱姆法则 若方程组的系数行列式$D\neq0$,则方程组仅有唯一解:$x_{i}=\frac{D_{i}}{D}$,$(i=1,2,…,n)$,其中$D_{i}(i=1,2,…,n)$是D中第i列元素$a_{1i},a_{2i},…,a_{ni}$换为方程组的常数项$b_{1},b_{2},…,b_{n}$后得到的行列式
对方程组:
$a_{11}x_{1}+a_{12}x_{2}+…+a_{1n}x_{n}=b_{1},$
$ a_{21}x_{1}+a_{22}x_{2}+…+a_{2n}x_{n}=b_{2},$
$……$
$a_{m1}x_{1}+a_{m2}x_{2}+…+a_{mn}x_{n}=b_{n}$
若$b_{1}=b_{2}=…=b_{n}=0$,则称该方程组为齐次方程组
$x_{1}=x_{2}=…=x_{n}=0$一定是方程组的解,这个解被称为方程组的零解,也叫平凡解
若一组不全为零的数是方程组的解,这个解称为非零解,也叫非平凡解
注意:
齐次方程组一定有零解,但不一定有非零解
若齐次方程组的系数行列式$D\ne0$,则方程组仅有零解
若齐次方程组有非零解,则$D=0$,反之亦成立

